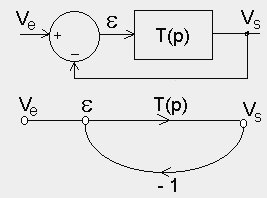
L'asservissement peut donc s'étudier comme étant un seul système, de fonction de transfert T(p), qui est bouclé. On peut en faire la représentation ci-contre:
La règle de Mason permet d'écrire immédiatement la fonction de transfert en boucle fermée:
W(p) = T(p) / [1+T(p)]
Mais T(p) est un rapport :  T(p) = n(p) / d(p) ,  ainsi il est plus facile d'exprimer W(p) en fonction de n et d :     W(p) = n(p) / [n(p) + d(p)]
Pour exprimer la fonction de transfert en boucle fermée il suffit d'ajouter le numérateur au dénominateur de la fonction de transfert en boucle ouverte.
En général nous connaissons T(p) sous une forme canonique factorisée puisque c'est un produit de fonctions de transfert (il suffit par exemple que le processus soit identifié par un modèle de Strejc).
Par contre n(p) + d(p) devient dans tous les cas un polynôme dont chaque coefficient dépend du réglage de gain du correcteur.
L'étude de cette fonction de transfert W(p) est donc souvent très compliquée. C'est pourquoi la théorie des asservissements est basée sur l'étude de la fonction de transfert T(p) en boucle ouverte afin d'en déduire les performances de l'asservissement (en boucle fermée).
Ainsi nous étudierons successivement la stabilité, l'amortissement, la précision et la vélocité des asservissements par l'examen de la fonction de transfert T(p) en boucle ouverte.
Bien sûr, dans les cas simples (premier ou second ordre) il est alors plus efficace de travailler sur la fonction de transfert W(p) en boucle fermée. Mais dès que l'ordre de T(p) est égal ou supérieur à 3 on ne calcule pas W(p). 
 

5.2  Stabilité de la boucle

Il est assez facile de comprendre qu'une boucle peut osciller puisque le système "se mord la queue!".
Supposons que la consigne reste constante et faisons l'hypothèse que la boucle engendre une sinusoïde (superposée à une constante). Nous allons comprendre que cette hypothèse peut se vérifier.
Une sinusoïde apparaissant en V_s se retrouve instantanément en e mais avec un déphasage de - 180° (signe moins du comparateur). Il suffit que, pour la pulsation de cette sinusoïde, l'ensemble correcteur-ampli-processus-capteur introduise à son tour un déphasage de - 180° pour qu'il y ait continuité
Remarque: Ceci ne peut être obtenu que si le processus est au moins d'ordre 3 (ou d'ordre inférieur avec un retard pur).
Si pour cette pulsation le gain de l'ensemble est égal à 1 la sinusoïde est auto-entretenue.
Si ce gain est inférieur à 1 la sinusoïde subit une décroissance exponentielle de son amplitude: dans ce cas la boucle est stable.
Si ce gain est supérieur à 1 la sinusoïde augmente en amplitude de façon exponentielle: dans ce cas la boucle est instable.
En pratique l'amplitude de l'oscillation ne peut pas augmenter indéfiniment car les saturations de l'amplificateur seront rapidement atteintes et la limiteront. Une oscillation d'amplitude constante mais non sinusoïdale sera alors observée: cette oscillation s'appelle pompage.