Ainsi la pulsation critique wc de l'oscillation sinuso´dale que la boucle peut créer est telle que T(jwc) = -1 (argument de -180° et module de 1).
La pulsation critique wc est donc définie par l'équation ^T(jwc) = -180°.
Rappel : dans ce cours le symbole ^ correspond à l'argument du nombre complexe.
Quatre cas sont possibles:
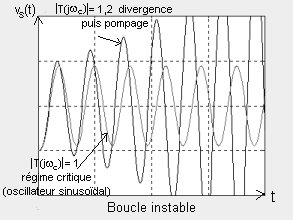
. Si šT(jwc)š > 1 : la boucle est instable, elle engendre une oscillation d'amplitude divergente jusqu'au pompage limité en amplitude par les saturations de l'amplificateur.
. Si šT(jwc)š = 1 : la boucle engendre une oscillation sinuso´dale. Mais il s'agit d'un régime critique: en pratique ce gain ne peut pas être rigoureusement égal à 1.
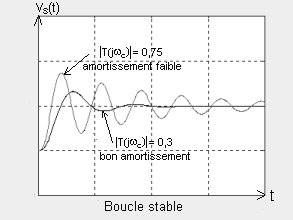
. Si šT(jwc)š < 1 mais proche de 1 (par exemple 0,75): la boucle est stable mais mal amortie (l'amplitude des oscillations diminue peu à chaque pseudo-période).
. Si šT(jwc)š < 1 nettement plus petit que 1 (par exemple 0,3) : la boucle est stable et bien amortie (en une pseudo-période on retrouve pratiquement un régime permanent constant).
Seulement dans ce dernier cas on peut considérer que le système bouclé est un asservissement.
 |  |
La valeur critique du nombre complexe T(jw) est donc -1.
On peut faire une étude graphique de la stabilité de la boucle en représentant le nombre complexe T(jw) (Nyquist ou Black) et en positionnant cette valeur -1 qui sera le point critique. Dans Bode le point critique devient deux axes critiques (-180° et 0 dB).
A la page suivante sont représentés les 4 cas ci-dessus décrits pour les 3 types de représentation d'un nombre complexe (Nyquist, Black et Bode).
![]()